Illustrations of the 4 most common Functions in School Mathematics


Straight Lines

Imagine buying a cup of coffee for a friend that cost $1.50, then imagine buying a 2nd cup of coffee for another friend. Thing about how much extra you spent for that 2nd cup. Okay, buy another cup for a third friend. It total you have spent $4.50 for 3 cups of coffee. The relationship that describes how the cost increases as you buy more and more cups of coffee is called a straight line relationship or linear function.



Parabola

Consider trying to organise a Round Robin Tennis Tournament with some friends. When you first start planning the tournament, only 4 of you seem to be able to make it. Then the day before, a 5th member joins and then on the day itself, your cousin is in town and he wants to play too!

How many matches do you need to arrange so that the tournament could take place with either 4, 5 or 6 players ?

The relationship between the number of players and the number of matches to be scheduled is parabolic, or forms a parabola when visualised.



Exponential 

Take a piece of A4 paper and fold it in half. How many equal partitions do you have ? Now fold it again and again observe the partitions. Finally fold it a 3rd time, what do you notice about the partitions and how they are changing? 


The relationship between the number of folds and the number of partitions is an example of what we call exponential growth or an exponential function. Population growth is often described using this type of relationship. 

Hyperbola 

Imagine buying a chocolate slab with 12 pieces. As you leave the shop where you bought it from, you run into a friend and you decide to stop and have a chat, so that you can share it with them. Then just as you are about to divide it up, another friend walks past and you decide you don't want this person to feel left out, so now you need to divide your chocolate into three equal sections.

Then just when you thought you were finally about to start eating your chocolate, your mom comes past and says she has a real sweet tooth. You cant leave your mom out , so now you need to divide your chocolate slab into 4 equal pieces.

What do you notice about how much each person gets, as you need to share it between more and more people? What do you notice about the overall relationship between no. of people sharing and no. of pieces of chocolate you each get?





Summary 

These 4 situations paint a real life picture of the most common relationships (Mathematical Functions) that students study at high school.

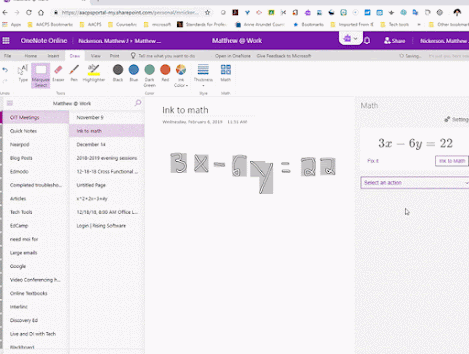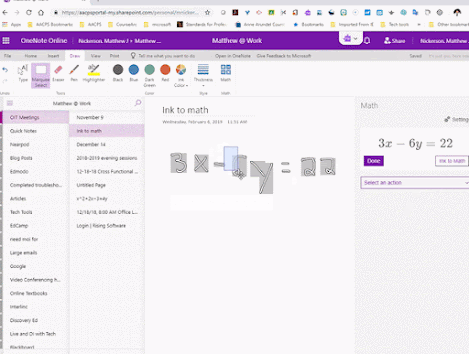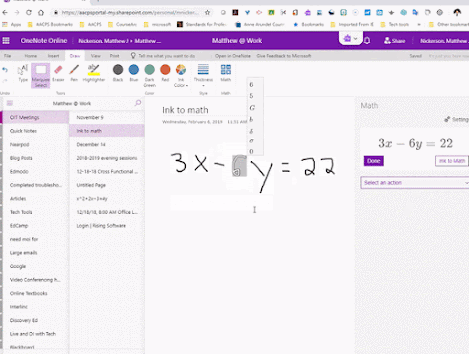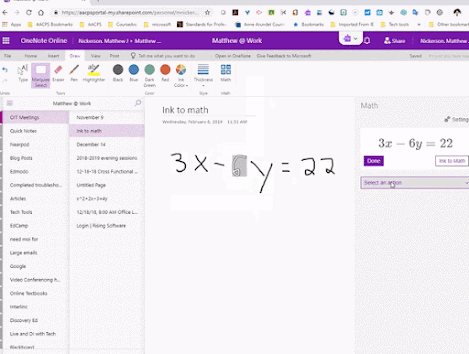
Comments

Post a Comment

Popular posts from this blog

Using Mathematics to Help Buy a Car in the South African Context (Part 2)

Image
Image Credit Follow on  In the previous post ( link to part 1 )  I discussed the basic mathematical  ideas to have in mind when thinking about purchasing a car. I had decided I would look at cars in the range of 80 - 100 000 rand and I wanted to buy a used car because of the better value offered. The videos in post 1, suggest cars around the range of 2 - 4 years old, as they offer the best trade off between future maintenance costs and depreciation on the purchase price after you have bought it. I agree with the facts laid out and will probably look for something in the 3 to 4 year old range. However I still need to check to see if the same patterns on maintenance costs and depreciation are also true in the South African context.  This points to our next step in our search. How do we get accurate information relevant to the SA context to see if these ideas mentioned are true and so allow me to get closer to my ultimate goal, buying a car. I am going to start with an internet search to
Read more

Finding Academic Information Efficiently

Image
  Intro Here are a collection of links that give great advice on how to track down academic information efficiently over time. It could be particularly helpful for postgraduate students who are finding the accessing and sorting of academic information overwhelming. https://paperpile.com/g/academic-search-engines /  https://paperpile.com/guides/research / https://paperpile.com/guides/writing/   https://paperpile.com/g/search-online-research-database/   https://paperpile.com/g/academic-research-databases/   https://paperpile.com/g/google-scholar-guide /  https://paperpile.com/g/search-online-research-database /  https://paperpile.com/g/eric-research-database/   https://paperpile.com/g/what-is-research-paper/   https://guides.library.ucla.edu/databases/choosing  
Read more

A little bit about OneNote for Maths Teachers

Image
Intro Over the last year or so I have increasingly been using Microsoft OneNote to author my maths lessons. I think a lot of maths teachers would benefit from having a closer look at the tool as it has a lot features that lessen the amount of work a maths teacher has to do when preparing lessons. It is also very easy to work with, when collaborating with other maths teachers because of the native sharing functions it has. Some Useful Links  These are a collection of links I saved to help with common problems I had when starting to use OneNote as Maths Teacher.  My Online Notebooks URL   (link to the online version) Export and Import Copies of OneNote Notebooks  Import Whole Notebooks into OneNote Online URL Great OneNote Youtube Tutoria l for Maths Teachers  Summary I plan to return to this post in future and update it as I continue using OneNote in my Mathematics Teaching in 2022. 
Read more